| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- ResNet
- super resolution
- 데이터 시각화
- 개 vs 고양이
- 장학프로그램
- Computer Vision
- kt디지털인재
- data analysis
- 태블로 실습
- 딥러닝
- Semantic Segmentation
- Deep Learning
- 데이터과학
- VGG16
- 파이썬 구현
- 데이터 분석
- SRCNN
- k-fold cross validation
- VGG
- Data Augmentation
- 논문리뷰
- kt희망나눔재단
- 논문 리뷰
- 태블로
- cnn
- 머신러닝
- object detection
- 데이터 증강
- sparse coding
- Tableau
- Today
- Total
기억의 기록(나의 기기)
[논문 리뷰 / Computer Vision] SRCNN - Image Super-Resolution Using DeepConvolutional Networks 본문
[논문 리뷰 / Computer Vision] SRCNN - Image Super-Resolution Using DeepConvolutional Networks
황경하 2024. 7. 12. 14:07Computer Vision - SRCNN
안녕하세요, 데이터과학을 전공하고 있는 황경하입니다.
오늘은 Super Resolution 분야에 딥러닝을 처음 적용한 SRCNN에 대해 공부해 보겠습니다.
해당 논문을 선택한 이유는 SRCNN에 대한 시초이자 교과서라고 많이 말씀을 하시더라고요. 그런데, 제 생각보다 난이도가 너무 높아서 정말 많은 분들의 블로그를 보며 도움을 받았습니다.
SRCNN은 Sparse Coding 기법을 Base로 하고 있습니다. 따라서, Sparse Coding에 대한 공부가 되지 않은 상태에서 이 글을 읽으시면, 이해가 어려울 수 있습니다. Sparse Coding에 대한 설명은 이 글에 남겨두었으니 참고부탁드립니다.
리뷰 논문: https://ieeexplore.ieee.org/abstract/document/7115171/
Image Super-Resolution Using Deep Convolutional Networks
We propose a deep learning method for single image super-resolution (SR). Our method directly learns an end-to-end mapping between the low/high-resolution images. The mapping is represented as a deep convolutional neural network (CNN) that takes the low-re
ieeexplore.ieee.org
* 이 글에 포함되는 모든 사진은 위 논문에서 발췌한 것임을 미리 밝힙니다.
* 해당 글에 설명은 논문을 기반으로 한 주관적 해석이므로 틀린 부분이 있다면, 댓글로 지적 부탁드립니다!
서론
논문에는 나와있지 않지만, Super Resolution의 뜻과 필요성을 정의할 필요가 있을 것 같습니다.
우리는 데이터를 수집할 때 항상 고품질의 데이터를 취득할 순 없습니다. 대용량의 데이터를 수집하기 위하여 때로는 드론에 초소형 카메라를 달아 수집을 하기도 하죠. 이렇게 수집된 이미지의 해상도는 카메라의 성능 때문에 매우 낮을 것입니다. 그러면, 이런 저품질 데이터로 학습한 모델의 성능 또한 낮아지게 되겠죠. 따라서, 수집한 이미지의 해상도를 끌어올려서 모델의 성능을 개선시키자는 것이 Super Resolution의 목적성입니다.
Super Resolution은 ill-posed problem입니다. 즉, 유일한 해가 존재하지 않는 문제라는 것이죠. 아래 그림처럼, 어떠한 사람은 HR 1을 어떤 사람은 HR2를 잘 복원이 되었다고 대답할 수 있습니다. 보통 이러한 경우에는 사전 정보를 통해 해가 나올 수 있는 경우의 수를 제한합니다. 우리가 배울 SRCNN은 Sparse Coding 방식에 기초되어 있으며, Sparse Coding 기법은 저해상도 이미지와 고해상도 이미지를 쌍으로 주어 해의 공간을 제한하고 있습니다. 이를 외부 예제 기반 방법 (external example-based strategy)이라고 합니다.
* Sparse Coding에 대한 자세한 설명은 이전 포스팅에 올렸으니 포스팅에서는 다루지 않겠습니다.

간단히 Sparse Coding 기법에 대해 요약하자면, 저해상도 이미지와 고해상도 이미지를 입력으로 받고, 저해상도 이미지의 패치와 고해상도 패치를 각각 인코딩합니다. 그리고, 아래처럼 저해상도 이미지의 패치들의 Linear Combination이 원본 저해상도 이미지가 되도록 하는 Basis를 학습을 통해 찾고, 그 Basis를 고해상도 패치들에 매핑하여 원본 고해상도 이미지가 되도록 합니다.

다만, 이 Sparse Coding의 문제점은 파이프라인의 최적화가 일부분만 된다는 것입니다. 즉, Basis를 찾는 과정은 최적화가 될 수 있지만, 그 외의 패치 추출, 매핑, Linear Combination 과정들은 그렇지 않다는 것이죠. 따라서, SRCNN에서는 Linear Combination은 결국 퍼셉트론과 같은 의미를 가지니 딥러닝으로 구현할 수 있고, 패치 추출과 매핑과정은 CNN에서 주로 하던 것들이니 CNN으로 구현하면, 역전파를 통해 모든 과정을 최적화할 수 있지 않을까 라는 아이디에서 시작되었습니다.
본론
SRCNN의 아키텍처는 매우 간단합니다. 고작 3층밖에 되지 않으며 중간에 Dropout과 같은 다른 층 없이 Convolution 층만 3개가 결합되어 있습니다. 아래와 같이 Patch Extraction -> None-linear mapping -> Reconstuction 층으로 3개의 Conv층만 존재합니다.

그럼에도, 성능은 기존 SOTA 방법들보다 더 뛰어나며 feed forward 아키텍처이므로 속도도 매우 빠릅니다. 뒤에서 나오겠지만, SRCNN의 층을 더 깊게 쌓거나 더 큰 데이터셋을 이용하여 성능 개선의 가능성도 제안되었지만, 층을 깊게 쌓는다면 모델의 복잡성이 올라가며 속도가 느려지고, 무조건 성능 개선을 보장하진 않았습니다. 아래는 기존 SOTA 방식들과 SRCNN의 성능 비교 그림입니다.

이전에는 고해상도 이미지로 복원하는 과정에서 컬러 스페이스를 제한하여 수행했었습니다. 예를 들어, RGB채널이 있더라도 YCbCr 또는 YUV 채널로 변경하고, luminance(광도) 채널의 이미지만 복원하는 등의 과정을 했었죠. 하지만, SRCNN은 Convolution 층을 통해 채널을 동시에 처리하기 때문에 RGB채널을 한 번에 처리할 수 있는 장점이 있습니다.
Formulation
논문에서는 저해상도 이미지를 Y라고 하고, 고해상도 이미지를 X라고 합니다. 그리고, 어떠한 함수 F를 Y가 거치어 X와 최대한 유사해지길 바라죠. 즉, F(Y) ~ X가 되도록 하는 F를 찾는 것이 목적입니다. 이 F를 찾기 위해서 위 아키텍처에서 본 Patch Extraction -> None-linear mapping -> Reconstuction 을 거치는 것입니다.
1) Patch Extraction: 패치를 추출하는 과정은 Sparse Coding 기법을 베이스로 하고 있기 때문에 반드시 필요한 과정입니다. 사실 이를 구현하는 방법은 매우 간단합니다. 우리가 CNN에서 Convolution 층의 작동원리를 보면, 필터가 이미지를 sliding window 방식으로 feature map을 추출하죠. 그 feature map들을 패치라고 생각하면, 그저 Convolution(Conv) 층 하나를 통과한 것과 같습니다. 식으로 나타낸다면, 아래와 같습니다. Y는 저해상도 이미지이고, W1은 첫 번째 Conv 층의 필터, B1은 Bias를 뜻합니다. 마지막에 max(0, ..)을 취해준 것은 Relu함수를 표현한 것입니다.

2) Non-Linear mapping: 첫 번째 Conv층에서 필터를 n1 * f1 * f1을 사용했다고 합시다. 그러면 F1(Y)은 n1 차원이 되겠네요. 이를 n2 차원으로 매핑하기 위해 이 non-linear mapping층을 거칩니다. 사실, 이렇게 차원만 변경하는 테크닉은 Computer Vision 태스크에서 많이 사용되고 있는 것 같습니다. 보통은 n2 * 1*1 필터를 사용하여 차원만 변경되도록 설계하는데요. 이 논문에서는 3*3, 5*5 필터와 같이 필터 크기를 더 키워서 진행합니다. 식으로 표현하면 그저 첫번째 Conv층을 통과한 결과에 한 번 더 Conv를 통과해 주고 Relu를 통과시키는 것밖에 없습니다.

3) Reconstruction: 마지막으로 이를 합쳐서 하나의 이미지로 만듭니다. 이 과정에서 Conv층을 통과하되 마지막에 활성화 함수를 Linear로 두어, Linear Combination을 표현하고 있습니다.

이를 그림으로 표현하면 아래와 같습니다.

Training
훈련 시 유일한 전처리 과정이 하나 있습니다. 바로, input image보다 output image의 해상도가 더 커야 하기에 upscaling을 해주는 과정입니다. 우리의 아키텍처는 모두 Conv층으로 결국 이미지의 크기를 작게 만드는 과정들입니다. 그렇기 때문에 이미지를 강제로 bicubic 보간으로 복원하면서 upscale factor만큼 키워줍니다.
논문에서 기본적으로 설정하는 하이퍼 파라미터는 f1 = 9, f2 = 1, f3 = 5, n1 = 64, n2 = 32 설정입니다. 또한, Loss는 MSE를 사용합니다. 즉, F(Y)와 X 사이에 각 픽셀값들의 차이를 최대한 줄이는 방식으로 학습하게 되죠.
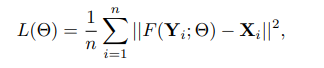
사실 MSE를 Loss를 설정하는 데에는 다른 이유도 있습니다. 일반적으로, Super Resolution에서 많이 사용한 metrics 중 PSNR이라는 지표가 있습니다. 이는 식을 보면 알 수 있듯이, MSE가 작아질수록 커지게 되죠. 즉, 모델을 MSE를 기준으로 학습시켜서 MSE 값을 최대한 낮추게 되는 모델이 가장 높은 PSNR을 받게 될 것입니다.

optimizer로는 stochastic gradient descente방식을 사용합니다. 그러나, 많은 구현 코드에서 Adam을 사용하더라고요. 실제로 Adam을 사용하는 것이 더 수렴 속도가 빠르고, 성능이 개선된다는 글을 본 적 있습니다.
그리고, Conv 층의 초기 가중치는 평균이 0, 표준편차가 0.01인 가우스 분포에서 추출하며, 학습률은 처음 두 개 층에서는 10^-4를, 마지막 층에서는 10^-5승을 사용합니다.
Training Data
총 91개의 이미지를 훈련 데이터로 사용합니다. 다만, 딥러닝을 사용하는 만큼, 데이터셋이 커질 때 더 나은 성능을 보이는지를 체크하기 위해 ImagNet dataset도 사용합니다.
우리는 하나의 이미지에서 크롭 하여 많은 패치들을 뽑아내죠. 따라서, 필터 사이즈를 33으로 잡고 패치를 추출하면 이미지는 91개이지만, 실제로 사용하는 이미지는 24,800개의 이미지가 됩니다. 그러면, ImageNet dataset은 500만 개 이상의 데이터를 사용하게 됩니다. 업 스케일링 계수는 3이며, 실제 두 데이터셋을 이용해 측정한 결과는 아래와 같습니다. 솔직히 저는 성능 하락을 예상했습니다. 신경망이 겨우 3층밖에 되지 않기 때문에, 훈련하기 위해서 시간이 훨씬 많이 걸릴 것이고, 데이터셋이 너무 크기 때문에 under fitting을 예상했는데, 성능이 오히려 더 좋게 나왔고, 훈련 시간도 비슷하다고 하네요. 왜지..?

Comparison
지금부터는 모델의 층을 더 깊게 쌓아보기도 하고, 필터의 크기를 늘려보기도 하고, 필터의 개수를 늘려보기도 하며 성능을 비교해 봅니다. 이 모든 과정을 다 글로 쓰기에는 힘들 것 같아 사진으로 대체하겠습니다.


첫 번째 사진은 층을 3개로 잡을 때와 4개로 잡을 때 얼마나 성능 차이가 있는지를 보여주고 있습니다.
보시다시피, 큰 차이가 없으며 층을 깊게 쌓는다고 반드시 드라마틱한 성능 개선을 보장하진 않는다는 것을 다시금 알려주고 있습니다. 층을 깊게 쌓으면 모델의 복잡성이 올라가니 오히려 층을 3개만 잡는 것이 더 효율적일 수 있겠네요. 이런 이유로 논문에서도 층을 3개만 쌓는 것을 추천합니다.
두 번째 사진에서는 층을 3개로, 4개로, 5개로 쌓았을 때와 필터 크기가 커지는 경우도 같이 나타내고 있는데, 결국에는 층을 3개 쌓은 것이 가장 좋은 성능을 보여줍니다. 이 결과는 91장의 사진을 기준으로 표현되었으며, 겨우 91장의 입력 이미지와 3개의 Conv층으로 이런 결과를 보인다는 것이 정말 신기합니다.
Comparison With SOTA
다음은, SOTA 기술들과 비교해 보겠습니다. 여기서 사용된 SRCNN 모델은 9-5-5로 층을 쌓았고, ImageNet dataset으로 훈련한 결과를 토대로 기술되었으며, 테스트 데이터는 Set5, Set14 dataset을 사용했습니다. PSNR에서 SRCNN은 거의 처음부터 bicubic 방식의 성능을 뛰어넘으며, 많은 훈련 후에는 압도적인 성능을 보여줍니다.
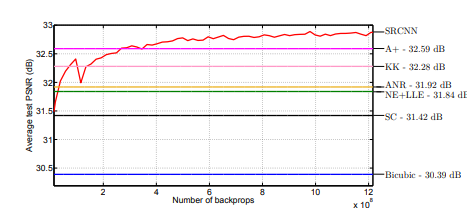
다른, metrics들에 대한 결과도 SRCNN이 더 좋은 성능을 보입니다.

마지막으로, SRCNN의 장점은 기존 SOTA 기법들과 달리 RGB 채널을 동시에 사용하는 것이라고 했죠. 따라서, 채널에 따른 PSNR값도 살펴보겠습니다. 우리가 예상하다시피, RGB채널을 모두 사용하는 경우가 SRCNN 모델의 최대 성능을 이끌어낼 수 있습니다. 이는 CNN의 특징이 아닐까 싶네요.

Insight
: 많은 블로그들에서 이 논문에 대한 리뷰를 남기고 있어, 짧게만 적어봤다. 어쩌면, 이 포스팅은 남에게 설명하기 보다 내가 리마인드할 때에 보려고 하는 것에 초점이 더 맞춰진 것 같기도 하다. 다양한 도메인에 DL을 처음 적용할 때에는 기존의 사용하던 원리들을 DL로 바꾸어서 사용하는 경우가 많은 것 같다. 어쩌면 당연한 것이지만, 결코 쉬운 것은 아니다. 이 논문을 보면서, 저자가 Sparse Coding의 매커니즘과 Convolutional layer의 매커니즘을 겹쳐서 생각했다는 점에서 놀랐다. 나라면 그럴 수 있었을까. 다시 생각해보면, Sparse Coding의 매커니즘을 알았다면, 연관지어 생각해볼 수도 있었을 것 같다. 다만, Sparse Coding 자체를 몰라서 못했을 것 같다. 다양한 분야에 관심을 갖고 깊게 살펴보면서, 어떻게 AI 기술 (ML, DL 등)
마무리..
오늘은 이렇게 SRCNN에 대해 살펴봤습니다. 사실 SRCNN을 보완한 여러 기법들이 존재합니다. 그래서, 이 정도로 멈추고 그다음 보완 기법들을 살펴보려 합니다. 그래서 일부러 좀 더 깊게 공부를 했는데, 이를 블로그에 표현하려 하니 글이 너무 길어지기도 하고 가독성이 떨어지는 것 같습니다.
오늘도 읽어주셔서 감사합니다.





