| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- kt디지털인재
- VGG
- super resolution
- Data Augmentation
- Computer Vision
- VGG16
- Deep Learning
- SRCNN
- 딥러닝
- 논문리뷰
- 데이터과학
- object detection
- 태블로 실습
- Tableau
- 논문 리뷰
- 데이터 시각화
- cnn
- 머신러닝
- data analysis
- 파이썬 구현
- k-fold cross validation
- 데이터 분석
- Semantic Segmentation
- 데이터 증강
- 태블로
- 개 vs 고양이
- 장학프로그램
- ResNet
- sparse coding
- kt희망나눔재단
- Today
- Total
기억의 기록(나의 기기)
[Sparse Coding] 희소 코딩 기법에 대한 그림을 통한 쉬운 설명 본문
[Sparse Coding 기법] - 쉬운 설명
안녕하세요, 데이터과학을 전공하고 있는 황경하입니다.
오늘은 다음 포스팅을 위한 사전 학습? 차원에서 Sparse Coding에 대한 설명을 해보려 합니다.
다음 포스팅은 SRCNN에 대한 논문 리뷰인데, SRCNN이 Sparse Coding을 베이스로 구현되었기 때문에 다음 리뷰를 읽으시는 분들에 편의를 위해 Sparse Coding 기법부터 설명해 보겠습니다.
*이 글에 포함된 내용은 논문과 블로그, AI ChatBot 등을 활용하여 얻은 지식들을 제가 이해한 대로 적은 것이므로, 틀린 해석이 포함되어 있을 수 있습니다. 만약, 틀린 부분이 있다면 댓글로 남겨주세요!
* 참고 논문: https://www.sciencedirect.com/science/article/abs/pii/S089360801500043X
참고 논문: https://ieeexplore.ieee.org/abstract/document/7115171/
Image Super-Resolution Using Deep Convolutional Networks
We propose a deep learning method for single image super-resolution (SR). Our method directly learns an end-to-end mapping between the low/high-resolution images. The mapping is represented as a deep convolutional neural network (CNN) that takes the low-re
ieeexplore.ieee.org
Sparse? Why Sparse Coding?
Sparse는 "희소하다"라는 뜻을 가지고 있습니다. 즉, 보기 힘든 귀한 상황을 이야기하죠. 그러면 Sparse Coding 기법에서 뭐가 희소하다는 것일까요? 이후에 설명할 내용을 보시면 더 이해가 편하시겠지만, 정답을 미리 말씀드리면, 희소 코드가 대부분이 0의 값을 가지므로 0이 아닌 값이 희소하다는 의미입니다.
Sparse Coding
희소 코딩 기법을 제대로 이해하려면 먼저 선형 대수학의 개념을 이해해야 합니다. Sparse Coding을 설명할 때에 사용되는 단어들 Basis, Linear Combination 등의 단어들이 모두 선형대수학의 개념이기 때문이죠. 쉽게 말해, Linear Combination은 Y = A * X1 + B * X2 + ... 의 식으로 Y를 표현하는 것을 말합니다. 이때, A, B, .. 등은 실수가 되며, 이를 모아서 벡터로 표현한 것을 Basis Vector(기저 벡터)라고 표현합니다. 그러면, [X1, X2, X3, ...]의 입력 벡터와 [A,B,...]의 기저 벡터를 곱한다면, Y가 된다는 것이죠. 이 방식이 희소 코딩의 주요 아이디어입니다.
희소 코딩은 대표적인 예제 기반 방법입니다. 저는 이미지 복원, 그중에서도 Super Resolution에 대해 공부하고 있으니 이 분야에 초점을 두겠습니다. (실제 희소 코딩의 활용도는 이뿐만이 아니라 인식, 노이즈 제거 등 많은 곳에서 사용될 수 있습니다.) 이미지 복원 기술은 ill-posed problem입니다. 즉, 유일한 해가 존재하지 않는 문제이죠. 예를 들어, 복원된 여러 사진들이 있을 때 어떠한 사람들은 1번 사진이 잘 되었다고 할 수 있고, 어떤 사람은 2번이 잘 되었다고 판단할 수 있습니다. 따라서, 우리는 해가 나올 수 있는 경우의 수를 제한할 필요가 있습니다. 그 방법 중에 외부 예제 기반 방법을 통해 저해상도 이미지와 고해상도 이미지를 쌍으로 주어 해를 제한하는 방법이 있습니다.
이렇게, 저해상도 이미지와 고해상도 이미지가 아래 그림처럼 주어진다고 합시다. 그러면, 저해상도 이미지에서 패치(작은 이미지)를 추출하고 Basis와 패치들의 Linear Combination의 결과가 원본 저해상도 이미지가 되도록 하는 Basis를 학습하게 되는 것이죠. 그리고 그렇게 나온 Basis는 고해상도 패치들을 결합할 때에 Basis에 매핑되어 그대로 사용하게 됩니다. 그러면, 고해상도 패치와 Basis의 Linear Combination이 아웃풋이 되어 고해상도 이미지가 되길 바라는 것입니다.
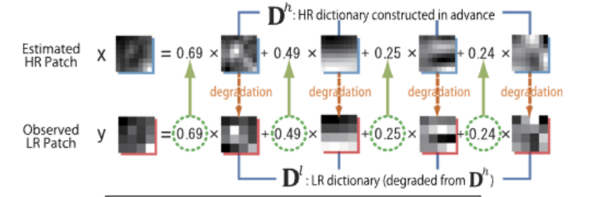
그럼 우리에게 남은 과제는 저 Basis를 어떻게 구하냐는 것입니다. 논문들에서 자세한 내용을 다루고 있진 않고 그저 OverComplete(과대 완전)될 수 있다고 설명합니다. 여기서 OverComplete는 입력 벡터(=패치 벡터) 보다 더 많은 Basis를 만든다는 것입니다. 예를 들어, 패치의 이미지가 8*8의 shape을 가진다고 합시다. 그러면, 총 64차원의 벡터가 만들어지게 되겠네요. 이 경우 원래 선형대수학이라면, Basis가 64차원이 되어 :Linear Combination을 수행해야 합니다. 그러나, 희소 코딩의 경우에는 Basis가 64차원이 아닌 128개, 256개, .. 등의 더 많은 후보군을 추출하게 됩니다. 그리고, 그 후보군은 대부분의 값이 0이고, 일부만 0이 아니며 그중 최소의 개수를 선택하게 됩니다. 그래서 "희소하다"는 표현을 하게 되는 것이죠. 이러한 방식으로 Basis Vector를 추출하게 됩니다.
그리고, 이렇게 만들어진 Basis는 고해상도 패치에 매핑되어 최종적인 output이 나오게 되는 것이죠.
문제점
Sparse Coding의 문제점은 부분 최적화 문제라는 것입니다. 즉, 모든 파이프라인에 최적화를 진행할 수 있는 것이 아니라, 특정 부분만 최적화를 할 수 있다는 것이죠. 여기서 특정 부분은 Basis를 추출하는 부분입니다. 다시 말하면, Basis를 추출하는 부분이 아닌 모든 과정은 사전/사후 처리되어야 한다는 것이죠. 패치를 추출하는 과정, Linear Combination을 하는 과정, 다시 고해상도로 Basis를 매핑하는 과정 등은 모두 학습과는 무관하다는 뜻입니다.
따라서, 이 모든 과정을 최적화할 수 있도록 만든다면 기존 희소 코딩 기법보다 더 나은 성능을 보일 수 있지 않을까 기대할 수 있습니다. 그것을 CNN을 통해 역전파를 통해 자동적으로 학습하게 만든 것이 SRCNN입니다. 이는 다음 포스팅이지만, 약간의 스포?가 되었네요. 내용이 끌리신다면, 이 글을 참고해 주세요. (아직 올리진 않아서 링크를 걸진 못 했습니다.)
Insight
: SRCNN 논문을 읽으며 나오는 단어인 Patch Extraction, non-linear mapping 단어들을 이해할 수 없어서 기반이라고 하는 Sparse Coding을 공부해봤다. 원래는 더 심오한 수학적 원리들이 들어있겠지만, 모델을 이해하는 데에 사용되는 원리는 이정도면 충분한 것 같다. 항상 새로운 모델들을 배우면서 느끼는 거지만, 모든 원리를 100% 다 알 필요는 없는 것 같다. 이것이 어디서 비롯되었고, 어떻게 만들어진 식인지까지 들어가게 되면 너무 딥하게 들어가버린다. 1,2학년 때는 깊게 배우면 좋은 게 아닌가? 하는 생각이 있었지만, AI는 1,2년 사이에 너무 빠르게 발전한다. SOTA model도 매년 바뀌고 이렇다 보니 모든 모델을 그렇게 딥하게 공부하기에는 시간이 너무 부족하다. 따라서, 요즘에는 모델의 아키텍처를 이해하고, 구현 코드를 이해할 수 있는 정도의 정보만을 습득하고, 더 다양한 경험을 해보는 것이 중요하다는 생각이 든다. 이번 Sparse Coding의 내용이 그렇게 딥하지 않은 것도 이러한 이유 때문이다.
마치며..
오늘은 Sparse Coding 기법에 대해 설명해 보았습니다. 많은 블로그들이나 논문에서 Sparse Coding을 설명하고 있지만, 저 같은 공부를 오래 해보지 못한 학부생 입장에서는 매우 어렵게 느껴지더라구요. 그래서 최대한 풀어서 설명하려 했는데 어떻게 느껴지셨을지 모르겠네요. SRCNN을 깊게 공부하기 위해서는 반드시 이해하고 넘어가야 할 부분이라 생각해 많은 자료를 참고해서 적은 내용입니다. 다음엔 SRCNN 논문 리뷰로 돌아오겠습니다 !
오늘도 읽어주셔서 감사합니다.

'딥러닝' 카테고리의 다른 글
| [Computer Vision] Dice, Jaccard Index 정의 및 차이점 (1) | 2024.11.18 |
|---|---|
| [Data Preprocessing] Duplicate Cleaner 소개 및 사용법 (1) | 2024.07.03 |
| [ResNet] 예제를 통한 설명 및 함수형 API 구현하기 (1) | 2024.06.25 |
| [VGG16] 예제를 통한 transfer learning, fine-tuning 설명 (0) | 2024.06.24 |
| [Data Augmentation] 예제를 통한 데이터 증강 효과 설명 (0) | 2024.06.24 |



